隨著全球變暖接近國際協議規定的極限,氣候行動的緊迫性日益增加。一項新的研究提供了全球氣溫上升的清晰可靠的記錄。它強調了世界距離突破《巴黎協定》的安全下限有多近。本說明強調需要簡單的定義,以便更容易跟踪實現國際氣候目標的進展。
格拉茨大學的 Gottfried Kir Chengast 和 Moritz Pichler 教授創造了 1800 年代中期至今全球地表溫度的新紀錄。它對未來十年做出了前瞻性預測。他們的研究成果發表在《通訊·地球與環境》雜誌上,展示了氣候變化的最新情況。報告顯示,最新年平均氣溫已升至《巴黎協定》規定的下限水平以上。與前工業化時代相比,即使兩年平均所顯示的長期變暖仍低於這條線,但研究得出的結論是,它很可能在這十年結束之前跨越。
Kirhengast 和 Pichler 教授開發了他們所謂的“ClimTrace 全球表面溫度記錄”,這是一個精心編制的數據集,旨在遵循政府間氣候變化專門委員會的方法。它是聯合國研究氣候問題的主要科學機構。同時,它使結果易於理解。通過調整陸地和海平面測量相結合的方法。他們發現了強有力的證據表明全球變暖在過去幾十年裡加速了。基爾成加斯特教授解釋說:“20年平均水平仍遠低於巴黎下限。但這一標準將在短短幾年內達到。”
該記錄不僅僅提供數字。但它也為如何設定和測量氣候限制提供了背景。例如,儘管最近的年平均數據顯示,全球變暖已經超出了巴黎設定的較低目標,但多年的長期平均數據顯示,在這一水平上持續變暖仍為時不遠。這些見解很重要,因為國際氣候政策依賴於長期平均值,而不是單年的極端高溫。
該研究還指出了一種更清晰的方式來解釋《巴黎協定》的進展情況。它引入了四個類別: 一年半的目標。這意味著與巴黎的主要目標保持一致。低兩度 這意味著略高於底部欄杆。但這一限制已被突破,足以在 2100 年之前實現明顯低於這一障礙的回報。低於 2 度的風險意味著接近 2 度。超過兩度意味著超過兩度。研究人員認為,這個簡單的系統將有助於決策者。法律專家和公眾可以更容易判斷世界是否履行承諾。
除了技術改進之外,這項工作還對全球行動具有重要影響。它提供的清晰度可以支持聯合國的全球盤點進程。這是對全球氣候進展的官方回顧。並作為氣候相關法律和法院案件的參考。基爾申加斯特教授表示:“這種精確的量化可以幫助促進跨政策和法律領域的氣候行動。進一步的標準化可以幫助支持《巴黎協定》的全球盤點進程。”
更大的信息令人擔憂:除了溫室氣體排放之外,這是指二氧化碳和甲烷等捕獲大氣中熱量的氣體。將迅速減少 世界將超越巴黎的界限,到達一個更安全的地方。並很快進入更危險的領域。預測表明,在不到十年的時間內,如果沒有更嚴重的行動。全球變暖可能會進入一個被認為處於危險之中的時期。長期形勢將表明本世紀全球變暖加劇。
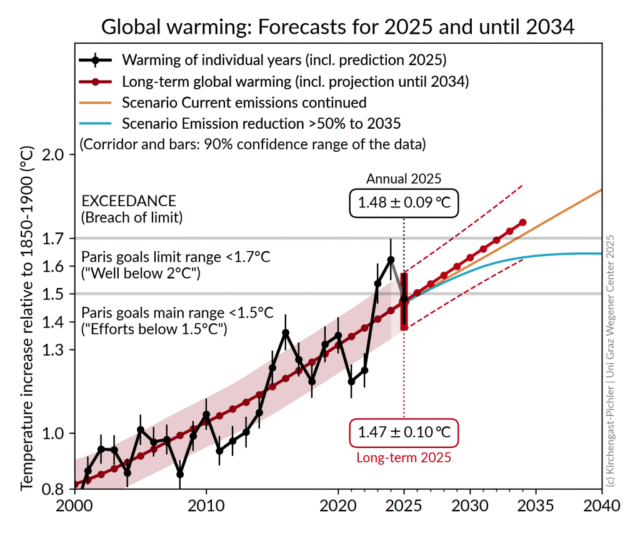
格拉茨大學的團隊也採取了緊急行動。 公佈今年的第一個預測。 在結束之前 他們的計算顯示,2025 年已接近巴黎的下限。這使得阻止全球變暖的時間所剩無幾。展望未來 他們預測,除非排放量大幅減少,否則世界幾乎肯定會在 2030 年之前超過 1.5 度的閾值。這是一個轉折點。因為焦點不僅僅轉移到過去的記錄上。但它也包括前瞻性預測,確認剩餘的機會之窗有多窄。
© Unigraz/韋格納中心
基爾成加斯特教授補充道:“確定明確、可量化的巴黎目標有助於促進跨政策和法律領域的氣候行動。我們的研究結果表明,這比以往任何時候都更加緊迫。”
期刊參考文獻
Kirhengast G.、Pichler M.“可追踪的全球變暖記錄和 1.5 °C 及 2 °C 以下溫度目標的清晰度”地球與環境通訊 2025 DOI: https://doi.org/10.1038/s43247-025-02368-0
紙質專題文章的後台信息 https://www.nature.com/articles/s43247-025-02368-0
關於作者

戈特弗里德·基爾琴加斯教授 是格拉茨大學首席科學家兼地球物理學教授(阿爾弗雷德·韋格納主席)。作為中國科學院國家空間科學中心(NSSC)名譽教授和2023年奧地利科學院院士,他獲得了許多其他獎項和獎項,包括施蒂利亞州科學、研究和藝術榮譽勳章,這是該州對社會終身科學成就的最高認可。他是格拉茨大學韋格納氣候與全球變化中心的創始主任。他是氣候變化卓越領域的創始講師。以及地球觀測和氣候戰略講師。奧地利國家氣候委員會的科學代表。除其他許多重要職責外,他(共同)發表了 400 多篇出版物,指導了 40 多名博士生,並在地球觀測和氣候科學領域做出了開創性研究和國際領導貢獻。

莫里茨·皮克勒 他擁有物理學理學碩士學位,專攻大氣物理學和氣候變化。自 2023 年起,他成為格拉茨大學韋格納氣候與全球變化中心格拉茨氣候變化指標團隊的研究員和博士生。他的工作重點是量化溫室氣體排放與全球變暖之間的物理聯繫,而他最近痴迷於“表面溫度”真正含義這個簡單但令人驚訝的複雜問題。